PC Hardware
We will focus on PC hardware, specifically 32 bit architecture, in this module. 32 bit architecture is a simpler than 64 bit architecture so makes for a gentler introduction. The principles and logic are the same for both.
Architecture
The main internal hardware of a PC consists of processor, memory, and registers. Registers are processor components that hold data and address. To execute a program, the system copies it from the external device into the internal memory. The processor executes the program instructions.
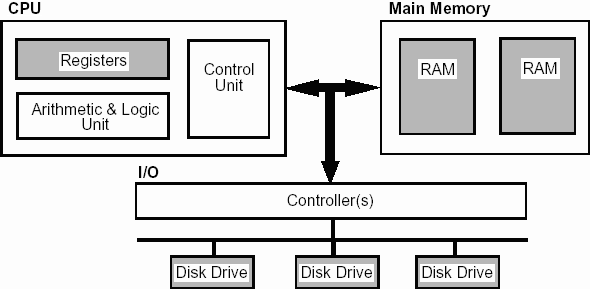
von Neumann Architecture
The image above is based on the von Neumann architecture. During the early days of computing the von Neumann architecture became dominant because it was robust in a time when the electronic components were unstable and short lived and it was easy to program.
The von Neumann architecture consists of a number of main components -
- Central processing unit (CPU) that executes instructions
- that are fetched from memory (which also stores data)
- by a control unit
- and an arithmetic logic unit (ALU) that performs computations
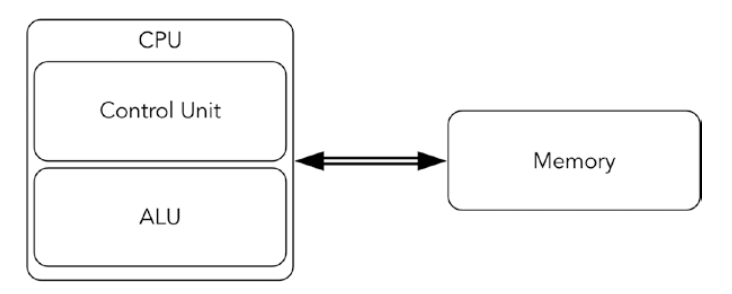
Key features
- Memory stores only bits
- Memory stores instructions and data. Instructions and data are indistinguishable
- Memory is organised in to indexed cells (typically bytes)
Advantages of Von Neumann Architecture
- Control Unit retrieves data and instruction in the same manner from one memory. Design and development of the Control Unit is simplified, cheaper and faster.
- Data from input / output devices and from memory are retrieved in the same manner.
- Organisation of memory is done by programmers which allows them to utilise the memory’s whole capacity.
Disadvantages of Von Neumann Architecture
- Parallel implementation of program is not allowed due to sequential instruction processing.
- Von Neumann bottleneck – Instructions can only be carried out one at a time and sequentially.
- Risk of an instruction being rewritten due to an error in the program.
Data Storage
The fundamental unit of computer storage is a bit; it could be ON (1) or OFF (0) and a group of 8 related bits makes a byte on most of the modern computers.
The processor supports the following data sizes −
- Word: a 2-byte data item
- Doubleword: a 4-byte (32 bit) data item
- Quadword: an 8-byte (64 bit) data item
- Paragraph: a 16-byte (128 bit) area
- Kilobyte: 1024 bytes
- Megabyte: 1,048,576 bytes
Binary (Review)
Every number system uses positional notation, i.e., each position in which a digit is written has a different positional value. Each position is power of the base, which is 2 for binary number system, and these powers begin at 0 and increase by 1.
The following table shows the positional values for an 8-bit binary number, where all bits are set ON.
| Bit value | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Position value as a power of base 2 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Bit number | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
The value of a binary number is based on the presence of 1 bits and their positional value. So, the value of a given binary number is −
1 + 2 + 4 + 8 +16 + 32 + 64 + 128 = 255
which is same as 28 - 1.
Hexadecimal (Review)
Hexadecimal number system uses base 16. The digits in this system range from 0 to 15. By convention, the letters A through F is used to represent the hexadecimal digits corresponding to decimal values 10 through 15.
Hexadecimal numbers in computing is used for abbreviating lengthy binary representations. Basically, hexadecimal number system represents a binary data by dividing each byte in half and expressing the value of each half-byte. The following table provides the decimal, binary, and hexadecimal equivalents −
| Decimal number | Binary representation | Hexadecimal representation |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
To convert a binary number to its hexadecimal equivalent, break it into groups of 4 consecutive groups each, starting from the right, and write those groups over the corresponding digits of the hexadecimal number.
Example − Binary number 1000 1100 1101 0001 is equivalent to hexadecimal - 8CD1
To convert a hexadecimal number to binary, just write each hexadecimal digit into its 4-digit binary equivalent.
Example − Hexadecimal number FAD8 is equivalent to binary - 1111 1010 1101 1000
Binary Arithmetic
The following table illustrates four simple rules for binary addition −
| (i) | (ii) | (iii) | (iv) |
|---|---|---|---|
| 1 | |||
| 0 | 1 | 1 | 1 |
| +0 | +0 | +1 | +1 |
| =0 | =1 | =10 | =11 |
Rules (iii) and (iv) show a carry of a 1-bit into the next left position.
Example
| Decimal | Binary |
| 60 | 00111100 |
| +42 | 00101010 |
| 102 | 01100110 |
A negative binary value is expressed in two’s complement notation. According to this rule, to convert a binary number to its negative value is to reverse its bit values and add 1.
Example
| Number 53 | 00110101 |
| Reverse the bits | 11001010 |
| Add 1 | 00000001 |
| Number -53 | 11001011 |
To subtract one value from another, convert the number being subtracted to two’s complement format and add the numbers.
Example
Subtract 42 from 53
| Number 53 | 00110101 |
| Number 42 | 00101010 |
| Reverse the bits of 42 | 11010101 |
| Add 1 | 00000001 |
| Number -42 | 11010110 |
| 53 - 42 = 11 | 00001011 |
Overflow of the last 1 bit is lost.
Addressing Data in Memory
The process through which the processor controls the execution of instructions is referred as the fetch-decode-execute cycle or the execution cycle. It consists of three continuous steps −
- Fetching the instruction from memory
- Decoding or identifying the instruction
- Executing the instruction
The processor may access one or more bytes of memory at a time. Let us consider a hexadecimal number 0725H. This number will require two bytes of memory. The high-order byte or most significant byte is 07 and the low-order byte is 25.
The processor stores data in reverse-byte sequence, i.e., a low-order byte is stored in a low memory address and a high-order byte in high memory address. So, if the processor brings the value 0725H from register to memory, it will transfer 25 first to the lower memory address and 07 to the next memory address.
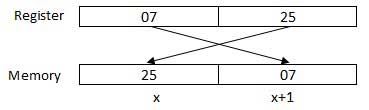
(Told you we’d come back to this!)
When the processor gets the numeric data from memory to register, it again reverses the bytes. There are two kinds of memory addresses −
- Absolute address - a direct reference of specific location.
- Segment address (or offset) - starting address of a memory segment with the offset value.