Binary Search Trees
Binary search trees are a special form of binary tree.. Binary search trees are sorted by an index or key value. This may be a value from node or calculated from it. This index value determines where a node is placed when it is added to the binary tree. Each node may have up to two children - a left child and a right child. The left child always has a lower index than its parent. The right child always has a higher index than its parent. (Where node with indexes equal to their parents are stored depends on the implementation. Typically nodes must have unique indexes and duplicate nodes are not possible).
// We will use the data value for the index in these examples
typedef struct node {
int data;
struct node *left;
struct node *right;
} node;
#include <stdlib.h>
node* CreateNewNode(int data)
{
node *temp = (node*)malloc(sizeof(node));
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
Adding A Node To A Binary Search Tree
Algorithm
- current node = root
- Is the current node == NULL?
- Y - Make the root node the new node, exit
- N - go to 2
- If the index of the new node less than the index of the current node?
- Y - is current node -> left == NULL
- Y - make current node -> left point to new node, exit
- N - make current node = current node -> left * N - is current node -> right == NULL
- Y - make current node -> right point to new node, exit
- N - make current node = current node -> right
- Go to 3.
To insert a new node in to a binary tree we traverse the tree, going left or right depending on how our new node’s index compares to the current node. When we would move to a null we instead replace it with the new node.
#include <stdbool.h>
void InsertNode(node **root, int data){
node *newnode = CreateNewNode(data);
if (*root==NULL)
{
(*root) = newnode;
return;
}
node *temp = (*root);
bool added = FALSE;
while (!added)
{
if (newnode->data < temp->data)
{
if (temp->left == NULL)
{
temp->left = newnode;
added = true;
}
else
{
temp = temp->left;
}
}
else
{
if (temp->right == NULL)
{
temp->right = newnode;
added = true;
}
else
{
temp = temp->right;
}
}
}
}
Traversing A Binary Search Tree
With a simple linked list we can traverse it (travel though it) by starting at the first node and moving to the next node repeatedly till we reach a NULL. We never have to think about the route we take through the tree, there are never any decisions to make. With a binary search tree at every node we have to decide whether to go left or right. And if we want to visit every node we have to visit both left and right. How do we do this? And how do we do it in some kind of order?
Well I’m afraid the answer is recursion. We can use recursion to visit every node in a binary search tree with a very simple recursive function.
void TraverseTree(node *anode)
{
// Test only needed for the first call when anode == root
if (anode!=NULL)
{
// if the current node has a left call TraverseTree(anode->left)
if (anode->left!=NULL)
{
TraverseTree(anode->left);
}
// if the current node has a right call TraverseTree(anode->right)
if (anode->right!=NULL)
{
TraverseTree(anode->right);
}
}
else
{
// should only come here if TraverseTree(&root) is called when root == NULL
printf("node is null\n");
}
}
The function above will visit every node in a binary search tree. It won’t do anything with any of the nodes, it just visits them. If we want to do something with each node, print out its data for example, then we would add code to the function to do it.
However where we add that code changes the order that things appear to happen.
Traversal Types
We typically refer to three types of traversal when dealing with binary search trees - In-Order, Pre-Order and Post-Order. The difference between the three is when we do stuff while traversing the binary search tree.
We can summarise the code above as
Traverse(node)
{
Traverse(left)
Traverse(right)
}
or for simplicity Traverse(left,right), we can then define the three types of traversal based on when we do stuff with each node.
- In-Order(left, do something, right)
- Pre-Order(do something, left, right)
- Post-Order(left, right, do something)
In the code example if we do something between the call to traverse left and to traverse right we are doing an in-order traversal. If we do it before we traverse left it is pre-order and if we do it after we traverse right it is post-order.
What difference does this make? Well consider the example below.
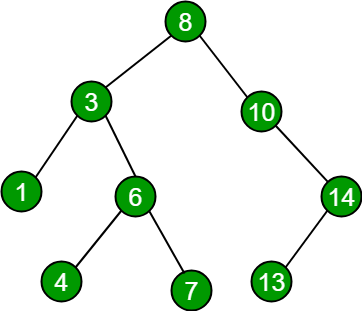
In-Order Traversal
In-order traversal is probably the most common way to traverse a BST because it visits the nodes in order from lowest to highest index.

An in-order traversal of a binary search tree acts upon the nodes in increasing value of index from the lowest value.
If we go with the simple example of printing out the data value as our “do something” then an in-order traversal of the tree above goes like this.
- Start at root (8).
- Go Left (3)
- Go Left (1)
- Can’t go left, output value [ 1 ]
- Can’t go right, go up (3) output value [ 3 ]
- Go right (6)
- Go left (4)
- Can’t go left, output value [ 4 ]
- Can’t go right, go up (6) output value [ 6 ]
- Go right (7)
- Can’t go left, output value [ 7 ]
- Can’t go right, go up (6) - we don’t output values when we travel up to a parent from the right.
- Go up (3)
- Go up (8), output value [ 8 ] - since 3 is 8’s left child
- Go right(10)
- Can’t go left, output value [ 10 ]
- Go right(14)
- Go left (13)
- Can’t go left, output value [ 13 ]
- Can’t go right, go up (14) output value [ 14 ]
- Go up (10)
- Go up (8)
- Finished
The resulting output, in order, is 1 3 4 6 7 8 10 13 14
The code to do this would be
void InOrderPrintNodes(node *anode)
{
// Test only needed for the first call when anode == root
if (anode!=NULL)
{
// if the current node has a left call TraverseTree(anode->left)
if (anode->left!=NULL)
{
TraverseTree(anode->left);
}
// InOrder Printing
printf("%d ", anode->data);
// if the current node has a right call TraverseTree(anode->right)
if (anode->right!=NULL)
{
TraverseTree(anode->right);
}
}
else
{
// should only come here if TraverseTree(&root) is called when root == NULL
printf("node is null\n");
}
}
Pre-Order & Post-Order Traversal
While pre-order traversal also favours travelling to the left over travelling to the right, it acts upon each node when it first visits them, resulting in a different order of actions.
void PreOrderPrintNodes(node *anode)
{
// Test only needed for the first call when anode == root
if (anode!=NULL)
{
// PreOrder Printing
printf("%d ", anode->data);
// if the current node has a left call TraverseTree(anode->left)
if (anode->left!=NULL)
{
TraverseTree(anode->left);
}
// if the current node has a right call TraverseTree(anode->right)
if (anode->right!=NULL)
{
TraverseTree(anode->right);
}
}
else
{
// should only come here if TraverseTree(&root) is called when root == NULL
printf("node is null\n");
}
}
The pre-order printing code above would produce a different output for the same tree.
8 3 1 6 4 7 10 14 13
It follows the same path through the nodes but acts on them immeadiately rather than after it can’t travel any further to the left.
Post-order traversal produces a third order
1 4 7 6 3 13 14 10 8
It travels as far as it can before outputting anything and only outputs the data from a node when the data from every node under it has already been output.
Searching a BST
To search for a node with a specific index value we start at the root node.
If the node we are on is NULL, then the node we are looking for is not present and we return NULL. If it isn’t NULL we compare the node we are on to the index value. If there is a match we return the node. If the index is less than the node’s index we move to the node’s left. If it is greater we move to the node’s right. We then repeat the process (from the start of this paragraph).
node* search(node **node, int val)
{
if((*node)==NULL) {
return NULL;
}
if(val == (*node)->data)
{
return *node;
}
else if(val < (*node)->data)
{
search(&((*node)->left), val);
}
else if(val > (*node)->data)
{
search(&((*node)->right), val);
}
}